Una función racional R(z) se define como el cociente de dos funciones racionales enteras, es decir, funciones polinomiales en que la variable no está afectada por exponentes negativos o fraccionarios.
Si el grado del numerador P(z) es igual o mayor que el del denominador Q(z), se tiene una fracción impropia; entonces, se debe dividir el numerador entre el denominador, para obtener una expresión mixta, es decir un polinomio y una fracción propia.
El último término es una función reducida a su más simple expresión, en el cual el grado del numerador P(z) es menor que el grado del denominador Q(z). Por último, debe integrarse término por término de la expresión mixta.
Este método tiene 4 casos los cuales se presentan a continuación:
Caso1:
Los factores del denominador son todos de primer grado y no se repiten.
En este caso, se tiene una descomposición en fracciones parciales de la forma:
Aquí no debe haber dos ai idénticas, y A, B,C,...,K, son constantes que van a ser determinadas. Se hace notar que el número de constantes por terminar es igual al gado del denominador.
Caso 2:
Los factores del denominador son todos de primer grado y algunos se repiten.
En este caso, el factor (z - a1) que se repite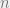 
veces, corresponde a la suma de n fracciones parciales de la forma:
veces, corresponde a la suma de n fracciones parciales de la forma:
Caso 3:
Los factores del denominador son lineales y cuadráticos y ninguno de los factores cuadráticos se repiten.
En este caso, a todo factor cuadrático 
, no repetido en el denominador, le corresponde una fracción parcial de la forma:
, no repetido en el denominador, le corresponde una fracción parcial de la forma:
El método para integrar expresiones de esta forma consiste en reducir la integral a una integral inmediata por sustitución algebraica.
Caso 4:
Los factores del nominador son lineales y cuadráticos y algunos de los factores cuadráticos se repiten.
En este caso, a todo factor cuadrático 
que se repite veces le corresponderá la suma de n fracciones parciales, de la forma:
que se repite 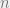veces le corresponderá la suma de n fracciones parciales, de la forma:
Ejemplo:
Obtener la transformada z inversa de la siguiente función
Solución. Expandiendo 
→ 
→ 
→ 
![\displaystyle x(k) = 4 \cdot Z^{-1} \left[ \frac{z^{-1}}{1-z^{-1}} \right] - 3 \cdot Z^{-1} \left[ z^{-1} \cdot \frac{1-0.5z^{-1}}{1-z^{-1}+z^{-2}} \right] + Z^{-1} \left[ z^{-1} \cdot \frac{0.5z^{-1}}{1-z^{-1} + z^{-2}} \right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+x%28k%29+%3D+4+%5Ccdot+Z%5E%7B-1%7D+%5Cleft%5B+%5Cfrac%7Bz%5E%7B-1%7D%7D%7B1-z%5E%7B-1%7D%7D+%5Cright%5D+-+3+%5Ccdot+Z%5E%7B-1%7D+%5Cleft%5B+z%5E%7B-1%7D+%5Ccdot+%5Cfrac%7B1-0.5z%5E%7B-1%7D%7D%7B1-z%5E%7B-1%7D%2Bz%5E%7B-2%7D%7D+%5Cright%5D+%2B+Z%5E%7B-1%7D+%5Cleft%5B+z%5E%7B-1%7D+%5Ccdot+%5Cfrac%7B0.5z%5E%7B-1%7D%7D%7B1-z%5E%7B-1%7D+%2B+z%5E%7B-2%7D%7D+%5Cright%5D&bg=f1f1f1&fg=666666&s=0&c=20201002 "\displaystyle x(k) = 4 \cdot Z^{-1} \left[ \frac{z^{-1}}{1-z^{-1}} \right] - 3 \cdot Z^{-1} \left[ z^{-1} \cdot \frac{1-0.5z^{-1}}{1-z^{-1}+z^{-2}} \right] + Z^{-1} \left[ z^{-1} \cdot \frac{0.5z^{-1}}{1-z^{-1} + z^{-2}} \right]")
Aplicando teorema de corrimiento para el segundo y tercer factor de las fracciones parciales resultantes
![\displaystyle x(k) = 4 \cdot Z^{-1} \left[ \frac{z^{-1}}{1-z^{-1}} \right] - 3 \cdot Z^{-1} \left[ z^{-1} \frac{1-0.5z^{-1}}{1-z^{-1}+z^{-2}} \right] + Z^{-1} \left[ z^{-1} \cdot \frac{0.5z^{-1}}{1-z^{-1}+z^{-2}} \right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+x%28k%29+%3D+4+%5Ccdot+Z%5E%7B-1%7D+%5Cleft%5B+%5Cfrac%7Bz%5E%7B-1%7D%7D%7B1-z%5E%7B-1%7D%7D+%5Cright%5D+-+3+%5Ccdot+Z%5E%7B-1%7D+%5Cleft%5B+z%5E%7B-1%7D+%5Cfrac%7B1-0.5z%5E%7B-1%7D%7D%7B1-z%5E%7B-1%7D%2Bz%5E%7B-2%7D%7D+%5Cright%5D+%2B+Z%5E%7B-1%7D+%5Cleft%5B+z%5E%7B-1%7D+%5Ccdot+%5Cfrac%7B0.5z%5E%7B-1%7D%7D%7B1-z%5E%7B-1%7D%2Bz%5E%7B-2%7D%7D+%5Cright%5D&bg=f1f1f1&fg=666666&s=0&c=20201002 "\displaystyle x(k) = 4 \cdot Z^{-1} \left[ \frac{z^{-1}}{1-z^{-1}} \right] - 3 \cdot Z^{-1} \left[ z^{-1} \frac{1-0.5z^{-1}}{1-z^{-1}+z^{-2}} \right] + Z^{-1} \left[ z^{-1} \cdot \frac{0.5z^{-1}}{1-z^{-1}+z^{-2}} \right]")
Pero 
